Labor Demand
The firms who sold goods and services in the unit on supply and demand now become the buyers in the labor market. Firms need workers to make products, design those products, package them, sell them, advertise for them, ship them, and distribute them, among other tasks. No worker will do this for free, and so firms must enter into the labor market and buy labor. Firms determine the amount of labor that they demand according to several considerations: how much the labor will cost (as represented by the market wage), and how much they feel they need, much in the way that buyers in the goods and services market buy according to the market price and their own needs.
Marginal Revenue Product
Firms are willing to buy labor up to the point where the marginal revenue product of labor is equal to the market wage. What does this mean? The marginal revenue product is the extra revenue a firm generates when they buy one more unit of input (in this case, the input is labor: a unit of labor isn't a new employee, it's another unit of work; an example would be an additional hour of work). As long as the income generated by extra hours of work balances (or exceeds) the wages paid for those extra hours of work, firms will be willing to pay for more labor.
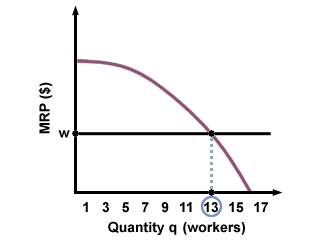
If the marginal revenue product (MRP) of labor is equal to the market wage, the firms will be at their optimal point of labor consumption, since buying more labor would mean that the MRP is less than the wage, and buying less labor would mean that the MRP is greater than the wage. If the marginal revenue product of labor is less than the market wage, then the firms are using too much labor, and those firms will probably cut back on the hours they buy until the MRP of labor is equal to the wage.
MRP > w : The firm will buy more labor
MRP = w : The firm is buying the right amount of labor
MRP < w : The firm is buying too much labor
Law of Diminishing of Returns
Why is this the case, that labor demand is at its optimal point when MRP of labor is equal to the wage? This holds true because of the law of diminishing returns. When a firm is hiring workers and deciding how many hours of labor it needs, it operates with the knowledge that the first hour added will make the biggest difference. For a while, every additional hour of labor for which a firm pays will yield a large marginal revenue. However, as the workers put in more and more time, each additional hour of work will yield less revenue. This phenomenon is true for several reasons: as the workers make more and more products, there may be a surplus, and not enough demand for the goods, in which case the marginal revenue would eventually fall to 0. Another reason underlying this fall in production is that after a certain point, extra workers and extra hours can be unproductive.
Imagine, for instance, that a small furniture store is hiring workers. One
worker will get a good deal done on his own. The second worker will probably be
productive, as well. The sixteenth worker, however, would probably get nothing
done, since there wouldn't be enough space or tools to make furniture. Between
the second and the sixteenth worker, we would see a gradual drop in marginal
productivity, a trend we call the Law of Diminishing Returns: additional workers
may add to productivity, but each worker contributes less, until the
marginal product (MP) is 0.
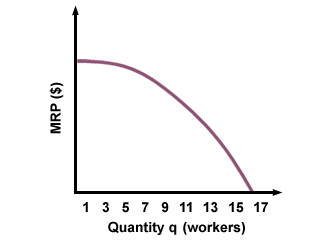
Because firms will logically hire a new worker or pay for extra hours only as
long as these actions will yield a net profit (MRP > w), we can assume that
their demand curve is going to be the same as the curve representing the MRP of
labor. This is because, as the MRP of labor falls, firms will hire less
additional labor. When the MRP is high, they will try to hire more workers for
more hours. Thus, we can use the MRP of labor curve to approximate a firm's
labor demand. The intersection of MRP with the wage determines how much labor a
firm is willing to hire:


 payment page
payment page



